1.5 SOLUTION SETS OF LINEAR SYSTEMS

1.HOMOGENEOUS LINEAR SYSTEMS

- Ax = 0으로 표현될때 Homogeneous 하다 라고 한다. (Ax = 0 Matrix equation을 Homogeneous linear system 이라 한다)

- trivial solution : x = 0 (분명한 solution)

- nontrivial solution : x = 0 이 아닌것 

 

- Homogeneous linear system 특징

1) 최소 하나의 trivial solution 을 갖는다. (= 원점을지난다)

2) nontrivial solution 갖는조건 : 방정식에서 free variable의 수가 적어도 하나 이상일 때, 즉 행렬의 rank가 변수의 개수보다 작을 때 (pivot 개수 < 변수의 개수)

 

- NonHomogeneous linear system : 원점을 통과하지 않는다. (Ax = b)

 

Ax=0을 augmented matrix로 표현하고 row reduction을 통해 reduced echelon matrix를 만들어서 free variable를 갖고 있는지 확인

 

- 이제 계산하는 방법을 알아보자

reduced echelon form으로 만들어서 해를 구한다.

x1 = 4/3 x3, x2 =0, x3 free

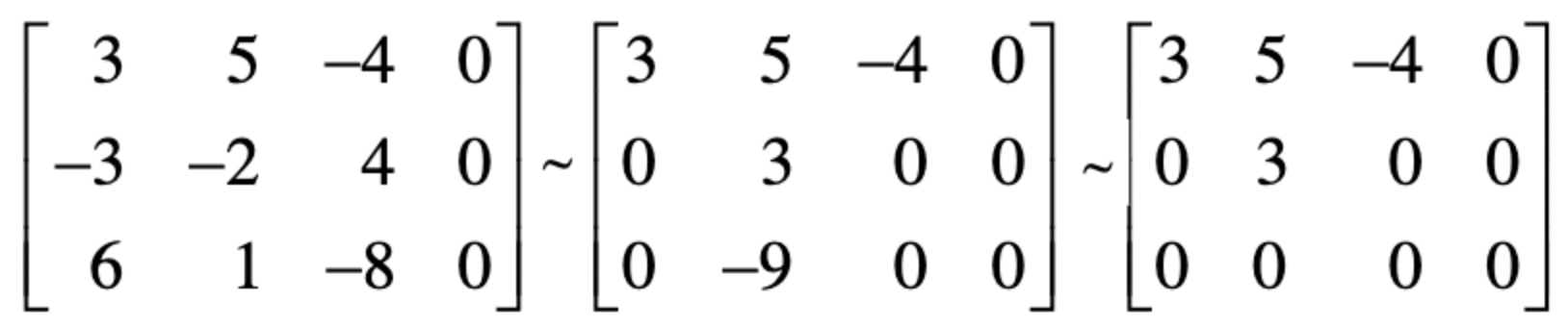
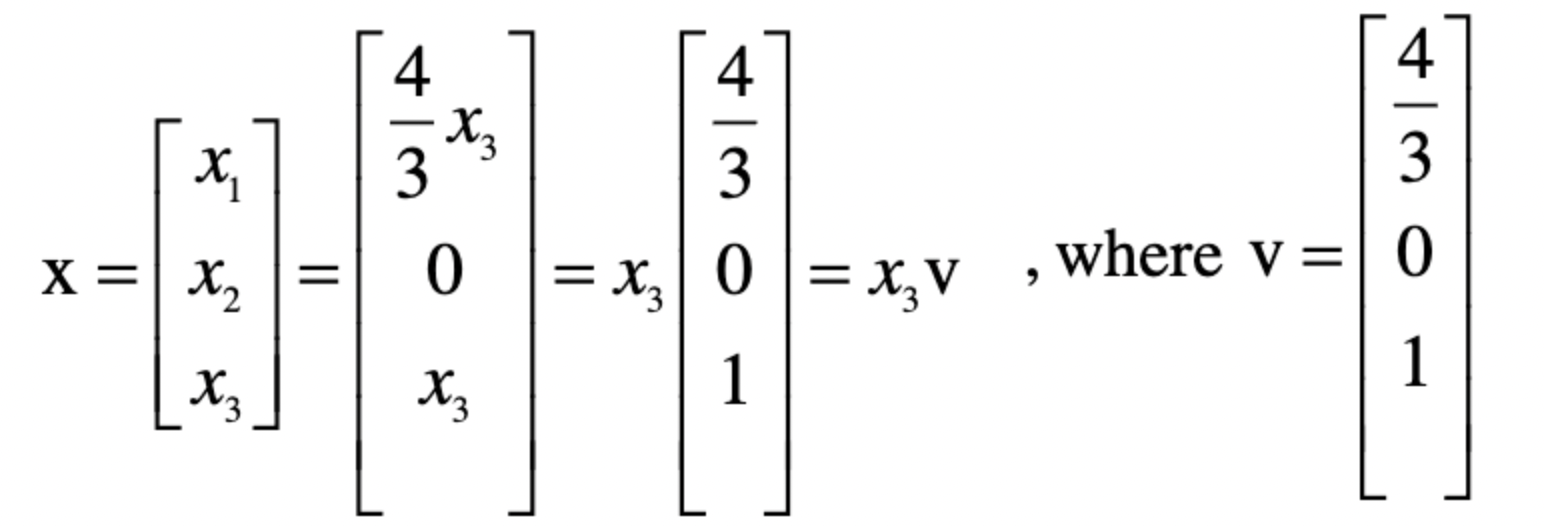
x1, x2, x3을 x3 하나로 표현할 수 있다 -> 하나의 벡터의 선형 결합으로 표현

• Span{v}를 의미하며 직선으로 표현
•  Span{v}로 표시할수 있다 -> nontrival solution가 존재
•  trivial solution은 x=0을 의미->  x에 해당하는 v가 사라지기 때문

---

2.SOLUTIONS OF NONHOMOGENEOUS SYSTEMS

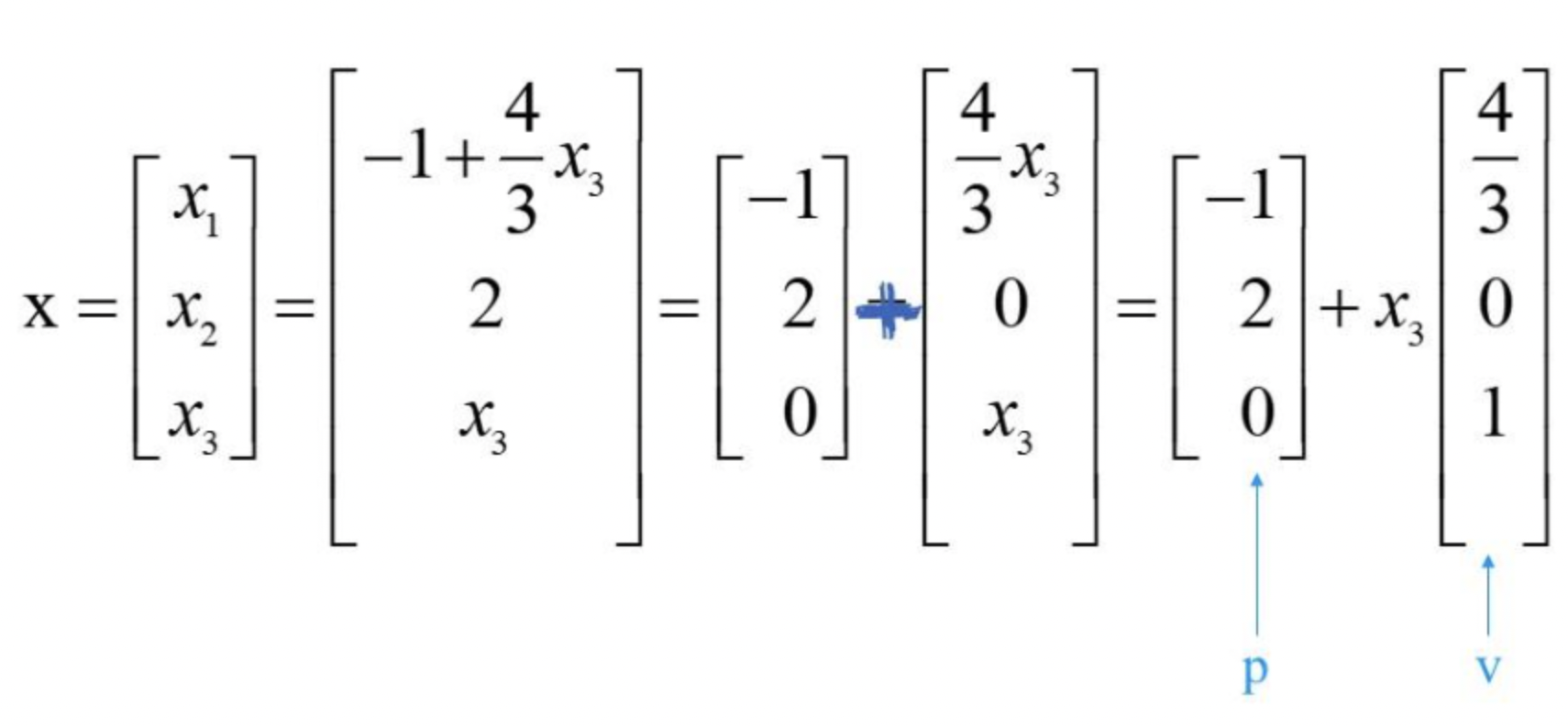
- non찾는법

1) homo로 찾고

2) 특수해 p를 찾는다

 

- Ax = b 일때, x = p + tv

-  Ax = 0 일때, x = tv

• Ax = b 해는 Ax = 0일때 해를 포함한당!
• Ax=b, Ax=0의 해는 p(particular solution)에 의해 평행 관계를 이룬다!!!!

평행관계!

 

 

(참고 : https://deep-learning-study.tistory.com/298)